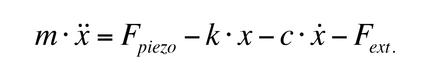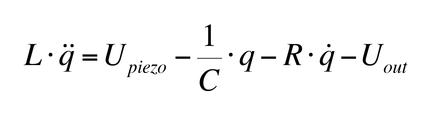The Mason model
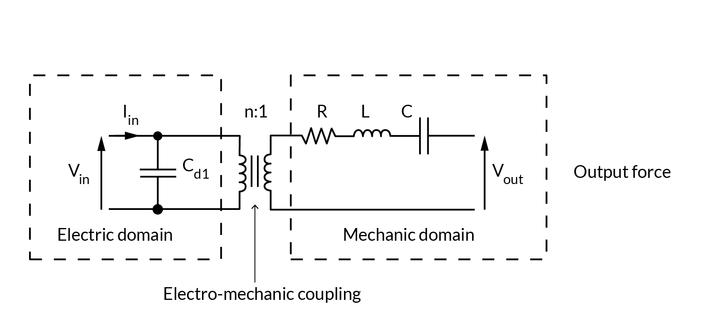
Since the dynamic system can be modeled using differential equations, there are a number of different ways to model, analyze and estimate the behavior. A very common method is to use a Mason model (similar to Butterworth-van Dyke equivalent circuit), which is an electrical equivalent of the equations of motion including the piezo effect.
The equation of motion can be written:
Which is the electrical equivalent
Electro-mechanical coupling (piezo effect)
This type of model can be extended to include more resonances, however in practice this is only useful for systems operating in a very wide frequency range.
Description of the parameters
Vin is the voltage applied on the piezo. This voltage is used to charge the electrical capacitance, and this way, generate a piezo force on the system.
The electro-mechanical coupling n describes the piezoelectric effect, i.e. the conversion of electrical energy to mechanical energy.
The system mass m is equivalent to an inductance L. This parameter describes the inertia of the system. A high value will drag the resonance frequency down.
The system stiffness k is equivalent to the inverse of a capacitance C. A high value of the stiffness (i.e. low value of the equivalent capacitance) will increase the resonance frequency of the system.
The system damping c is equivalent to a resistance R. Damping depends mostly on the materials used. High damping will lead to a slower but more stable step response. In an oscillating application, damping will reduce the overshoot around resonance but will lead to increased heat dissipation.
Identification of the parameters
There are different ways of identifying the parameters of a dynamic system.
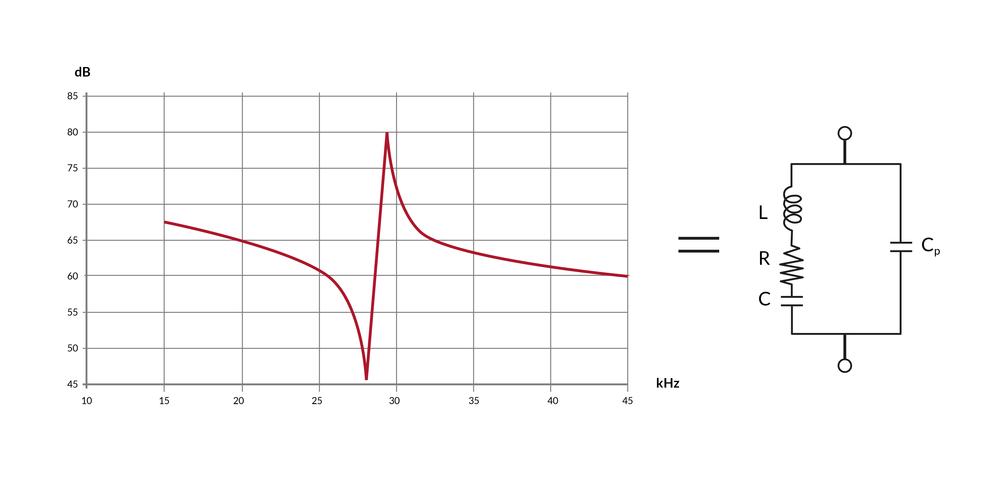
A common method is to measure the impedance spectrum of the piezoelectric element. Because of the electro-mechanical coupling, mechanical resonances are visible on the spectrum and can be modeled.
However, this method has two major drawbacks. First, it is only applicable for small signals and dynamic parameters tend to change for large signal. Second, it can only identify four parameters, therefore one is missing to relate the electrical equivalent to the mechanical domain.
Methods based on large signal excitation and direct measurement of mechanical parameters (typically displacement) provide more accurate models. There are different methods; the most common one is to measure amplitude and phase of the displacement for an electrical excitation at different frequencies (Bode plot). Parameters can also be identified based on the step response of the system.
Impendance spectrum
Sign up for our webinars
Our free 1.5 hour webinars follow the same structure as our tutorials.
A piezo partner - what do we mean by that
We give you a competitive advantage by using our extensive knowledge to customize and optimize your piezo products. Thus, we will be your long-term piezo partner. Send your request today.
Search tool
Performance
Dimensions
Value
Max operating voltage / V
Min
Min free stroke / µm
Min
Min estimated blocking force / N
Min
Min
Max
Length or outer diameter / mm
Min
Max
Width or inner diameter / mm
Min
Max
Max height / mm
Max
Product category
Choose here...
- Plate actuators
- Plate stacks
- Ring actuators
- Ring stacks
- Plate benders
- Ring benders
- Shear plate actuators
- Shear stacks
- 2D actuators
- High temperature stacks
- Damage tolerant stacks
Material
Choose here...
- NCE51
- NCE51F
- NCE46
- NCE57
- NCE40
- NCE41
- NCE55
- NCE56
- NCE59
- NCE81
- 0,00
- AA
- Material
- Type
- 0.00
Search
Clear
Next